Il codice binario è un sistema di codifica posizionale, simile a quello decimale ma che utilizza la base 2 per la rappresentazione dell’informazione.
Il Bit (Binary Digit) è l’unità elementare dell’informazione trattata da un elaboratore, e possiamo considerare il bit una variabile che può assumere solo due valori: 0 e 1.
L’ importanza del codice binario nei sistemi informatici è grazie al contributo di George Boole, che per primo è riuscito a semplificare i processi logici a delle espressioni formate da 0 ed 1.
Questo sistema di rappresentazione dell’informazione, ci permette di esprimere tramite questi due soli numeri qualsiasi cosa, seguendo delle convenzioni chiamate codifiche.
Nei computer infatti, ogni cosa viene salvata come una sequenza di zero ed uno: era sicuramente più chiaro prima dell’avvento dell’interfaccia grafica ovvero quando l’unica cosa che era possibile usare era una CUI (Character User Interface, conosciuta anche come CLI – interfaccia da linea di comando).
Pensate per esempio al vostro gioco per pc preferito, ai vostri film e alle vostre canzoni: tutte queste sono esempi di codifiche che dal lato della macchina non sono altro che una sequenza di zero ed uno.
Vediamo ora come rappresentare un numero decimale in binario, e come successivamente ritrasformarlo in decimale.
Rappresentazione binaria di un numero decimale
Ovvero: cambio di base
Da piccoli, ci insegnano a contare in modulo 10: contiamo 0,1,2,3,4,5,6,7,8,9 e poi ricominciamo il conto, aggiungendo una decina.
Il conto in binario, è simile: essendo però in modulo 2, i numeri sono solo 0,1. Quindi invece che 2, avremo 10, invece che 3, avremo 11 e così via.
Mentre per numeri piccoli potremmo pensare di fare i conti a mano, sarebbe abbastanza scomodo per quelli più grandi. Vediamo quindi come eseguire il cambio di base per un numero di arbitraria grandezza:
Dato il nostro numero in base 10, lo dividiamo per 2 finchè non finisce il resto. Il numero binario sarà dato proprio dai resti presi dalla fine all’inizio.
Quindi (nota: nella tabella, il due in alto a destra è per impostare la divisione):
| Risultato | Resto |
|---|---|
| 5234 | 2 |
| 2617 | 0 |
| 1308 | 1 |
| 654 | 0 |
| 327 | 0 |
| 163 | 1 |
| 81 | 1 |
| 40 | 1 |
| 20 | 0 |
| 10 | 0 |
| 5 | 0 |
| 2 | 1 |
| 1 | 0 |
| 0 | 1 |
5234, in binario, equivale a 1010001110010.
Possiamo immaginare la memoria del computer come una fila di scatole che possono contenere o zero o uno. Ogni scatola, rappresenta un bit.
Se con “cn” intendiamo una stringa binaria lunga n bit, l’ultimo bit a destra in posizione c0 viene chiamato LSB (Less Significant Bit – Bit meno significativo) mentre quello in posizione cn (ovvero il primo) viene chiamato MSB (Most Significant Bit – Bit più significativo).
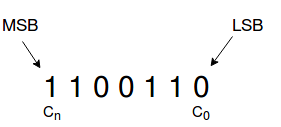
Operazioni aritmetiche: addizioni e sottrazioni in binario
Le addizioni in binario sono identiche a quelle in decimale:
1+1 = 10 10+10 = 100 11 +10 = 101
E’ ovviamente più facile farle impostandole in colonna
0001 + 0001 = 0010
Lo stesso vale per le sottrazioni.
1-1 = 0 10-10=0 11-10=1
Le moltiplicazioni:
1*0 = 0 1*1 = 1 0*0 =0
E le divisioni:
1/1=1 0/1=0
Conversione da binario a decimale
Per effettuare la conversione contraria, ovvero da un numero binario a decimale, basta seguire quanto segue:
Dato un numero binario ad esempio 111, l’equivalente in decimale è dato dalla somma:
22 + 21 + 20 = 4+2+1 = 7
111 in binario equivale quindi a 7. Il procedimento consiste nel effettuare la potenza di 2 elevato alla posizione della cifra. Dopo di che si sommano tutti i risultati.
Attenzione però: bisogna eseguire l’operazione usando solo i bit che valgono uno.
Vediamo un altro esempio per chiarire meglio le idee:
101= 22 + 0 + 20 = 5
La posizione del bit, contando da destra verso sinistra, indica a che potenza di due equivale. In questo caso:
- Partendo da destra, il primo bit è in posizione zero quindi vale
20 = 1 - Il secondo bit vale zero quindi non si conta (altrimenti sarebbe
21 = 2) - Il terzo bit è in posizione 2, quindi equivale a
22=4
Vediamo un altro esempio:
10101110: sono 8 bit. L’ equivalente in decimale è dato dalla somma di:
27 + 0 + 25 + 24 + 23 + 22 + 21 + 0 = 348
Sapendo il numero di bit, possiamo anche predire che range di numeri possiamo rappresentarci: il calcolo è semplice, dati n bit possiamo rappresentare al massimo 2n -1 numeri.
Nell’ ultimo esempio, usavamo 8 bit: il massimo numero che possiamo rappresentare con 8 bit è 28 -1 ovvero 256. Quindi, con 8 bit, possiamo rappresentare 256 “informazioni” diverse
In informatica, quando parliamo di 8 bit ci riferiamo più semplicemente ad 1 byte.
Per essere precisi, dovremmo riferirci ad 8 bit col nome di Ottetto in quanto con byte ci si riferisce per definizione all’ unità minima trasferibile: esistono infatti (vecchi) computer che con 1 byte si riferiscono a 7 bit.
Kilobyte e Kibibyte
Il sistema internazionale (SI) ha stabilito che con il termine kilobyte, ci si deve riferire (come per le altre unità di misura) a 103 byte.
Per riferirsi invece a 210byte dovremmo utilizzare il termine più preciso kibibyte: i produttori di hard disk, indicano la dimensione dello stesso utilizzando la definizione precisa “GigaByte”. Il nostro computer invece, per indicare lo spazio disponibile, utilizza erroneamente il termine gigabyte intendendo invece gibibyte.
Si ringrazia Mattyw per la precisazione di questo paragrafo 🙂
A proposito della notazione
Infine, una piccola precisazione di notazione: con KB ci si riferisce a KiloByte, con Kb si riferisce a kilobit. La differenza è nella “b” minuscola (bit) o maiuscola (byte).







Io veramente mi ricordavo che i kilobyte (prefisso SI) equivalessero a 1000 byte (idem per gli altri prefissi, che vanno sempre in base10 secondo il SI), mentre per le forme a base2 si utilizzassero i kibibyte (2^10 byte = 1024 byte)
Ottimo ho corretto l’articolo! Ti ringrazio molto per la segnalazione Mattyw 🙂
Federico