Il teorema CAP, è uno dei teoremi fondamentali dei sistemi distribuiti. Iniziato come una congettura fatta dal computer scientist Brewer (e per questo conosciuto anche come Brewer’s theorem), è diventato un teorema grazie a Seth Gilbert e Nancy Lynch del MIT i quali hanno dimostrato formalmente la congettura.
Sostanzialmente dice che un sistema distribuito può avere al massimo due di queste tre proprietà:
- Consistenza (Consistency): Ogni richiesta di lettura effettuata da qualunque nodo per lo stesso dato, porta allo stesso valore (o uno più aggiornato).
- Disponibilità (Availability): Ad ogni richiesta corrisponde una risposta. Ma senza la garanzia di ricevere risposte corrette (ovvero che le nostre letture siano coerenti).
- Tolleranza di partizione (Partition Tolerance): Il sistema continua ad operare nonostante arbitrarie perdite di messaggi fra i nodi.
Il teorema CAP afferma che un sistema distribuito non può essere contemporaneamente consistente, disponibile e tollrante al partizionamento. Vediamo prima quindi nel dettaglio in cosa consistono queste proprietà.
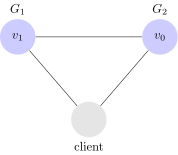
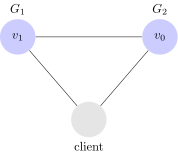
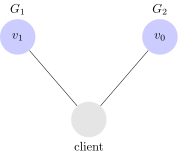
Un semplice sistema distribuito
Consideriamo quindi un semplice sistema distribuito. Il nostro sistema di esempio, è composto da due sever $latex G_1$ e $latex G_2$. Entrambi i server sono incaricati di tenere traccia di una unica variabile $latex v$, il cui valore iniziale è $latex v_0$. $latex G_1$ e $latex G_2$ possono comunicare tra di loro o con un client esterno.
Possiamo quindi visualizzare il nostro sistema così:
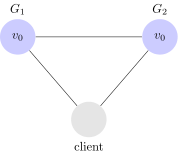
Un client può richiedere di scrivere (write) o leggere (read) la variabile $latex v$ ad entrambi i server. Quando un server riceve una richiesta, esegue la computazione necessaria e genera una risposta al client.
Ecco quindi un esempio di scrittura (write):
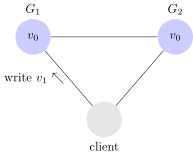
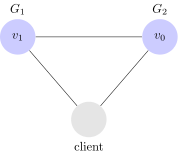
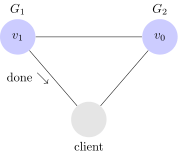
Ed un esempio di lettura (read):


Stabilite le caratteristiche del nostro sistema, passiamo a vedere nel dettaglio le proprietà di consistenza, disponibilità e tolleranza al partizionamento.
Consistenza
Vediamo come Gilber e Lynch definiscono nel loro paper la consistenza:
Qualunque operazione di lettura che inizia dopo una operazione di scrittura completata, deve ritornare quel valore o il risultato della successiva scrittura.
In un sistema consistente quando un client scrive un valore in un qualunque server e riceve una risposta di conferma, si aspetta che le successive richieste di lettura risultino nel valore da lui scritto o un valore aggiornato (ad esempio da un altro client) indipendentemente dal server interrogato.
Vediamo un esempio di sistema inconsistente:

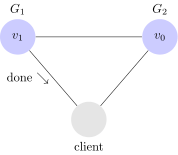

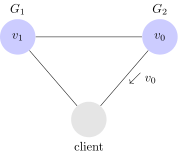
Il client scrive $latex v_1$ su $latex G_1$ che risponde con un ack (done). Quando però il client invia una richiesta di lettura a $latex v_2$, riceve dei dati non aggiornati: ovvero $latex v_0$.
Vediamo quindi un esempio di sistema consistente:
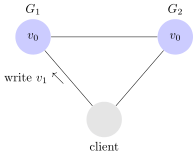


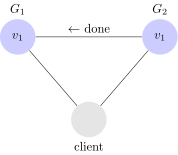

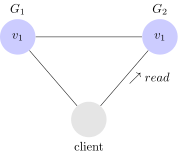

In questo sistema, $latex G_1$ replica il valore ricevuto su $latex G_2$ prima di rispondere con un ack al client. In questo modo, quando il client invia una lettura verso $latex G_2$, riceve il valore più aggiornato: ovvero $latex v_1$.
Disponibilità
Vediamo come Gilbert e Lynch descrivono la disponibilità di un sistema:
Ogni richiesta ricevuta da un nodo non fallito nel sistema, deve ricevere una risposta.
In un sistema ad alta disponibilità, se il client invia una richiesta ed il server non è crashato, allora deve ricevere una risposta. Il server non può ignorare le richieste del client.
Tolleranza al partizionamento
Gilbert e Lynch descrivono la proprietà di partition tolerance come:
Alla rete è permesso perdere un numero arbitrario di messaggi inviati da un nodo all’altro.
Questo significa che uno o più messaggi scambiati fra $latex G_1$ e $latex G_2$ potrebbe andare persi. Ammesso che tutti i messaggi vengano scartati, il sistema assomiglierebbe a questo:
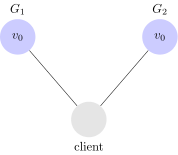
Se possiede la proprietà di partition tolerance, il nostro sistema deve riuscire a funzionare correttamente nonostante partizioni del network arbitrarie.
Dimostrazione del teorema
Dopo aver visto brevemente le proprietà di consistenza, disponibilità e tolleranza al partizionamento possiamo finalmente provare che un sistema distribuito non può possederle contemporaneamente tutte e tre.
La dimostrazione procede per assurdo: assumiamo che esista un sistema che possieda tutte e tre le proprietà.
Iniziamo creando una partizione del sistema:

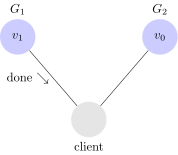
Un cliente invia a $latex G_1$ un comando di write per il valore $latex v_1$. Visto che il nostro sistema è disponibile, $latex G_1$ è obbligato a risponderci. Visto che la rete è partizionata però, $latex G_1$ non può replicare il valore appena scritto su $latex G_2$. Gilbert e Lnch chiamano questa fase di esecuzione con $latex \alpha_1$.

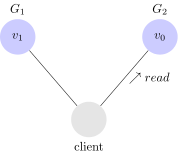
In seguito, il nostro client invia una richiesta di lettura verso $latex G_2$. Visto che il sistema è dispoibile, $latex G_2$ è costretto a rispondere. Visto che la rete è partizionata però, $latex G_2$ on ha potuto aggiornare il suo valore da $latex G_1$. Per questo motivo, ritornerà il valore $latex v_0$.
Gilbert e Lynch chiamano questa fase di esecuzione $latex \alpha_2$.
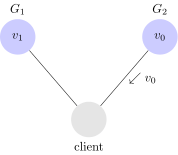
Ritornando il valore $latex v_0$ nonostante il client abbia inviato una write con un valore più aggiornato, $latex G_2$ rompe la proprietà di consistenza.
Visto che abbiamo assunto consistenza, disponibilità e tolleranza al partizionamento possano esistere contemporaneamente in un sistema, mostrando un esempio di esecuzione che rompe la proprietà di consistenza abbiamo dimostrato che non è possibile possederle tutte e tre insieme.
Per approfondire
Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services
Le immagini sono prese da: https://mwhittaker.github.io/blog/an_illustrated_proof_of_the_cap_theorem/





