In un mondo ideale, se il tempo di esecuzione di un programma su un singolo processore è $latex t_s$, vorremmo che il tempo per eseguire lo stesso programma su $latex n$ processori fosse $latex t_s/n$. Ma questo non è mai il caso!
In questo articolo vediamo le leggi di Amdhal e di Gustafson, che pongono dei limiti teorici sulla riduzione del tempo di esecuzione che possiamo raggiungere dalla parallelizzazione di un programma altrimenti eseguito in maniera sequenziale.

Efficienza e speedup

Iniziamo con definire il termine speedup. Con speedup si intende la riduzione prevista nel tempo di esecuzione di un programma. Dati:

  • $latex t_s$ = Esecuzione del programma in maniera sequenziale su un singolo processore.
  • $latex n$ = numero di processori
  • $latex t_n$ = tempo di esecuzione su n processori

Allora possiamo definire lo speedup come

$latex S_n = \frac{t_s}{t_n}$

Da cui è evidente che se $latex t_n = \frac{t_s}{n}$ allora lo speedup sarà di $latex n$.

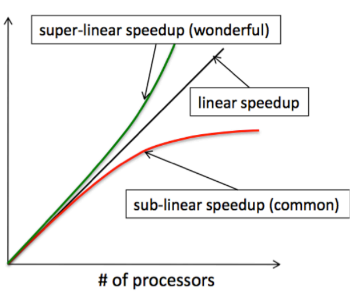
Uno speedup sub-lineare è il risultato più comune che possiamo ottenere dalla parallelizzazione di un programma.

Passiamo poi a definire l’efficienza, che altro non è che un uso effettivo dei processori:

$latex E_n = \frac{S_n}{n} = \frac{t_s}{n*t_n}$

Legge di Amdhal

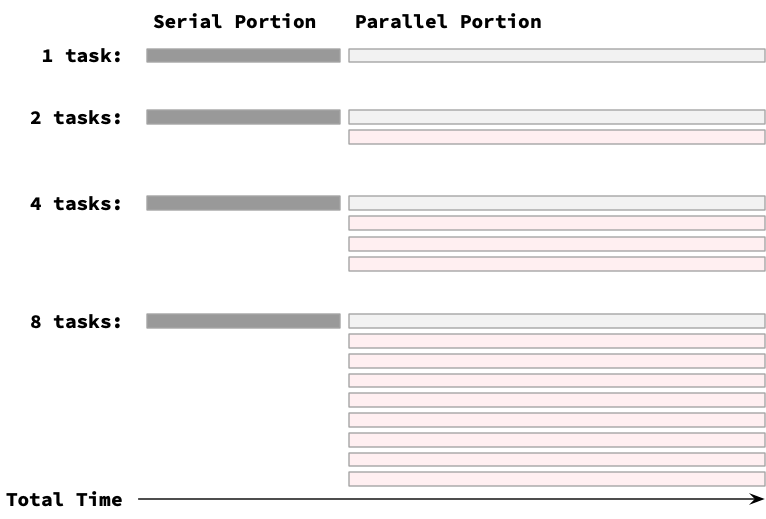
Tutti i programmi paralleli contengono porzioni di codice eseguito in maniera sequenziale e porzioni che verranno poi eseguite in maniera parallela.

La porzione sequenziale del codice limita l’efficacia della parte parallela. Questo perchè una volta deduplicati i tempi di esecuzione della parte parallela, la porzione sequenziale finirà per dominare il tempo di esecuzione; ponendo un limite superiore allo speedup possibile.

La legge di Amdhal, nota anche come strong scaling, incapsula questo concetto in maniera formale.

Formulata nel 1967 dal computer scientist Gene Amdhal, la formula è composta da:

  • $latex f$ = frazione seriale del programma – non parallelizzabile
  • $latex 1-f$ = La parte parallelizzabile
  • $latex n$ = numero di processori
  • $latex t_n$ = tempo di esecuzione su n processori

Data una applicazione parallela in cui f è sequenziale, il massimo speedup raggiungibile su n processori è dato da:

$latex S(n) <= \frac{1}{f+\frac{1-f}{n}}$

Se calcoliamo il limite di questa funzione con $latex n$ tendente ad infinito, $latex 1-f$ viene cancellato da $latex n$ e abbiamo:

$latex S(\infty) = \lim_{n \to \infty} S(n) = \frac{1}{f}$

Secondo la legge di Amdhal, una volta raggiunto il limite massimo di parallelizzazione, la parte di codice sequenziale determinerà il limite inferiore del tempo di esecuzione.

Vediamo un esempio: un programma eseguito su un singolo processore ha bisogno di 20 ore per essere eseguito. Una parte di codice di questo programma, richiede 1 ora (5%) per essere eseguita, mentre le restanti 19 (95%) possono essere parallelizzati. Questo vuol dire che, anche se avessimo infiniti processori, il wallclock time non potrà essere minore di un’ora, risultando in uno speed up teoretico di 20x al massimo.

Prima immagine su InformaticaLab generate artificialmente 🙂

Legge di Gustafson

Nel 1988, Gustafson notò che i ricercatori tendevano a cercare di sfruttare al massimo il potere computazionale a loro disposizione, dando in pasto alle loro macchine dei workload di dimensione maggiore. Ovvero, Invece di cercare di eseguire le stesse analisi in tempo minore, i ricercatori che avevano accesso a una quantità aggiuntiva di core tendevano invece a compiere più computazioni nella stessa quantità di tempo.

Ed è qui che è importante notare che la legge di Amdhal è a prima vista molto pessimista nei confronti del parallelismo, ma è perchè assume un workload costante. La legge di Gustafson invece suggerisce che aumentando il numero di processori e aumentando la dimensione del workload in input possiamo, nella stessa quantità di tempo, risolvere problemi più grandi.

Dati:

  • $latex n$ = numero di processori
  • $latex a$ = parte sequenziale
  • $latex b$ = parte parallela, eseguita da uno degli $latex n$ processori.
  • $latex a+b$ = tempo parallelo su n processori
  • $latex a+n*b$ = tempo totale di esecuzione seriale. E’ formato dalla parte seriale sommata alla unità eseguita da ogni processore moltiplicato per il numero di processori.
  • $latex \alpha =a/a+b$ = la frazione sequenziale del tempo di esecuzione parallelo

Allora lo speedup si può definire come $latex S(n) <= \alpha + n(1- \alpha ) = n – \alpha (n-1)$.

All’aumentare del numero di processori n, possiamo analizzare un workload maggiore nella stessa quantità di tempo.

Vediamo un esempio di utilizzo

$latex a =25% =$ parte sequenziale
$latex b =75% =$ parte parallela
$latex n =512$
$latex \alpha = 25/(25+75) = 0.25 $
Gustafson speedup = S (512) = 512–511* 0.25 = 384.25

Conclusione

Le leggi di Amdhal e Gustafson studiano i limiti teorici raggiungibili dalla parallelizzazione di un programma. La realtà però è spesso anche peggiore: il tempo necessario alla coordinazione di vari processi è maggiore di zero – avendo infiniti processi, passeremmo tempo infinito nella loro creazione. Anche avendo un grosso numero di processi (minore di infinito), il tempo di spawn dei processi e la loro sincronizzazione richiede tempo che ridurrà quindi l’efficienza. E’ interessante notare che superato un certo limite aggiungere nuovi processi renderà il programma più lento. Questo considerazioni prevedono che i problemi risolti dai vari processi non si sovrappongono: altrimenti c’è anche da aggiungere il tempo necessario a coordinare i processi (locks).

Referenze

  • Multicore systems programming della Prof. Irene Finocchi: https://drive.google.com/file/d/1fCYrMtQhtEiT4zXa5PwENTxDQ1bI6hZ3/view
  • Parallel Programming Concepts: Amdahl’s Law: https://cvw.cac.cornell.edu/parallel/synch
  • Reevaluating Amdahl’s Law: http://www.johngustafson.net/pubs/pub13/amdahl.htm
  • Amdahl, G.M. Validity of the single-processor approach to achieving large scale computing capabilities. In AFIPS Conference Proceedings vol. 30 (Atlantic City, N.J., Apr. 18-20). AFIPS Press, Reston, Va., 1967, pp. 483-485.