Vediamo prima a grandi linee cosa si intende per O grande, e poi ci addentreremo con definzioni un po più formali:

La notazione O grande (Big-O in inglese) è probabilmente una delle più importanti in Computer Science: questa indica il caso peggiore del tempo di esecuzione di un algoritmo.

Esistono altre notazioni, anch’esse importanti, che indicano ad esempio l’andamento di un algoritmo nel caso migliore e nel caso medio. Solitamente però, studiando un algoritmo, viene da domandarci quale sia il tempo di esecuzione nel caso più sventurato possibile.

Vediamo ad esempio questo algoritmo che ritorna True se a ∈ A:

algo contenutoIn (A [array di n interi], a intero da cercare) -> boolean
{
    if n == 0:
        return False
    for ogni elemento i in A:
        if i == a:
            return True
    return False
}

Quanto tempo impiega per essere eseguito? Per capirlo, analizziamo il numero di istruzioni (ad alto livello) che vengono eseguite:

algo contenutoIn (A [array di n interi], a intero da cercare) -> boolean
{
    if n == 0: //1 volta
        return False //1 volta
    for ogni elemento i in A: // n volte
        if i == a: // 1 volta per iterazione
            return True //1 volta
    return False //1 volta
}

Il maggior tempo di esecuzione viene speso all’interno del ciclo while che esegue, nel caso peggiore, al più n confronti (A è un array lungo n).

Per questo motivo, l’algoritmo contenutoIn ha tempo di esecuzione $latex O(n)$. Il caso migliore invece è se l’intero a da ricercare si trova in prima posizione in A. In quel caso l’algoritmo ha costo costante, e si scrive $latex \Omega(1)$ (si legge Omega, in inglese è consciuto come Big Omega).

Vediamo invece un esempio di listato che cerca due doppioni all’interno di un Array:

algo doppioni( A [array di n interi]) -> A senza doppioni
{
    for $latex \forall x \in A$: //1
        for $latex \forall y \in A$: //2
            if x == y:
                remove(A[y])
    return A
}

Che tempo di esecuzione ha questo algoritmo?

Il primo for esegue $latex n$ iterazioni. Il for (2) al suo interno esegue, per ogni iterazione del for esterno, n iterazioni. Per questo motivo, questo algoritmo ha tempo di esecuzione nel caso peggiore $latex O(n^{2})$
Inoltre questo programma esegue nel caso migliore $latex n^{2}$ iterazioni e, come abbiamo visto prima, si scrive $latex \Omega(n^{2})$.
Visto che sappiamo che il caso migliore è uguale al caso peggiore, per questo algoritmo possiamo concludere che il suo tempo di esecuzione è esattamente $latex n^{2}$, e si scrive $latex \theta(n^{2})$ (si legge theta di n^2).

Volendo dare alcune definizioni più formali:

Dicendo che un algoritmo A è O grande (o semplicemente O) di un algoritmo B, intendiamo dire che A nel caso peggiore si comporta come B.

Ovvero:

f(n) ∈ O(g(n))

O più comunemente si scrive:

f(n) = O(g(n))

Per definizione:

f(x) è asintoticamente uguale a g(x) se { g(x) : ∃ c1 >0, ∃ x0  tale che 0< f(x) < g(x)c1 per ogni x > x0}

In pratica significa che se esiste una costante c che moltiplicata per la funzione g(x) ci faccia diventare questa funzione maggiore di f(x) da un certo punto x0 in poi, allora diremo che f(x) è un O grande di g(x).

Ad esempio, prendiamo le due funzioni:

f(x) = 4x2 + 2x + 4
g(x) = 3x2

Per input molto grandi, x2 è il fattore che dà la spinta maggiore e via via “2x + 4” influiscono sempre meno.

Quindi, potremmo dire che (vale, ripeto, per input grandi):

f(x) = 4x2
g(x) = 3x2

basta prendere come costante c=2 per esempio:

f(x) = 4x2
c*g(x) = 2* 3x2 = 6x2

E ci accorgeremo che nel grafico di f(x), g(x) rappresenta un limite superiore. In parole povere: nel caso peggiore, f(x) si comporterà come g(x),

e che f(x) = O(g(x))

Per rendere tutto più chiaro: su Google è possibile visualizzare i grafici delle funzioni:

Andando verso destra si vede che nel primo caso f(x) ha una impennata maggiore rispetto a g(x). Applicando c a g(x) nel secondo grafico è possibile notare che f(x) viene battuta.

A cosa serve la notazione Big-O?

Dando un limite superiore (upper bound) stiamo definendo un limite massimo di risorse che verranno utilizzate dal nostro algoritmo. Es. L’algoritmo eseguirà al massimo n confronti.

Dando un limite inferiore (lower bound) stiamo definendo un limite minimo di risorse che verranno utilizzate dal nostro algoritmo. Es. L’algoritmo eseguirà almeno n confronti.

Con risorse si intende, ad esempio, il tempo di esecuzione dell’algoritmo (in termini di istruzioni da eseguire) o ancora la quantità di spazio necessaria per l’esecuzione dell’algoritmo.

Questa notazione ci è molto utile quando, dati dei requisiti, dobbiamo decidere il tipo di algoritmo o struttura dati utilizzare. Per farci un’idea, bigocheatsheet.com ci dà un paragone di molti algoritmi e strutture dati, con i loro rispettivi O grande per varie operazioni.

Una cosa importante è capire i vari ordini di grandezza, e sempre su bigocheatsheet abbiamo un’immagine molto esplicativa:

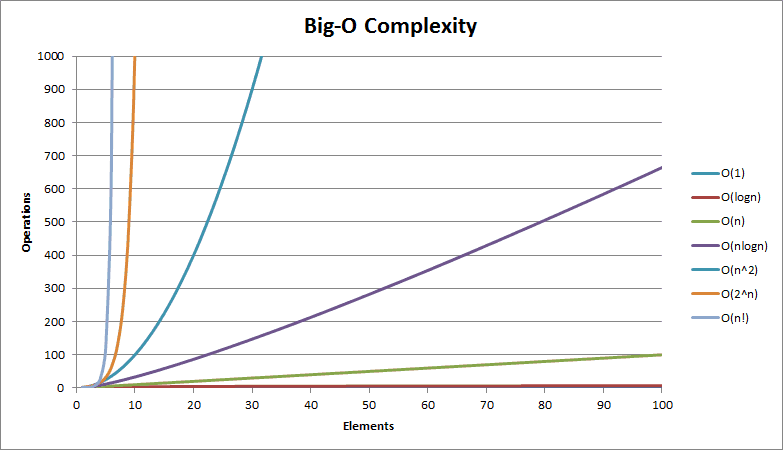
big-o-complexity

Conclusione

I concetti dietro ad O grande sono derivati dalla matematica. O Grande è la notazione di Landau che viene usata per descrivere il comportamento asintotico di una certa funzione. In questo post si fa ovviamente riferimento al concetto dal lato interessante per lo studio degli algoritmi, ma l’idea è la stessa. Per i più curiosi la pagina di Wikipedia (in inglese) approfondisce molto l’argomento.