L’ InsertionSort è uno degli algoritmi più facili da intuire che ci siano: si basa sullo stesso flusso di pensiero che ci porta ad ordinare meccanicamente un mazzo di carte da gioco.

InsertionSort, dal inglese ordinamento per inserimento, presentato ad alto livello funziona infatti così:

Abbiamo un mazzo di carte non ordinato.
Peschiamo una carta.
Peschiamo una carta e la confrontiamo con la precedente: se maggiore o uguale la posizioniamo a destra, altrimenti, se minore, a sinistra.
Peschiamo una terza carta, ripetiamo i confronti con le altre due e la inseriamo nel giusta posizione.
Ripetiamo con tutte le carte del mazzo, finché non avremo in mano tutte le carte ordinate dalla carta più piccola alla carta più grande.

E’ effettivamente questo il procedimento seguito dall’algoritmo di InsertionSort e per farlo non ha bisogno di creare array di supporto, quindi si dice che è un algoritmo In Place.

Lo spazio occupato infatti è $latex Theta(1)$.

Nei casi peggiori e medio, il tempo di esecuzione è di $latex O(n^2)$ che è veramente inefficiente, ma si presta molto bene ad ordinare insiemi già quasi ordinati.

Esempio di esecuzione:

Vediamo un esempio con un array di numeri:

Array di Interi A: [1,4,5,3,2]

Applichiamo l’algoritmo, di cui vedremo fra poco il codice, a questo array:

  1. [1, 4, 5, 3, 2] Inizia osservando l’elemento in posizione A[0], ovvero 1. Visto che non ci sono altri elementi, questo non viene spostato.
  2. [1, 4, 5, 3, 2] L’elemento in posizione A[1], ovvero 4, viene confrontato con 1. Essendo maggiore, viene posizionato alla destra di 1 (in questo caso, non cambia posizione).
  3. [1, 4, 5, 3, 2] A[2] = 5 viene considerato. Inizia a confrontare il 5 con 4, ed essendo 5 > 4, viene posizionato alla destra del 4.
  4. [1, 4, 5, 3, 2] A[3] = 3 viene considerato. Inizia a confrontare il 3 con il 5, ed essendo 3 < 5, si passa al confronto successivo. 4 > 3? Si, quindi si passa al confronto successivo. 1 > 3? No, quindi il 3 viene inserito alla destra dell’ 1.
  5. [1, 3, 4, 5, 2] A[4] = 3 viene considerato. Inizia a confrontare il 2 con il 5, ed essendo il 2 minore di 5, si passa al confronto successivo, fino ad arrivare al confronto con 1. Essendo 2 > 1, il 2 viene sistemato alla destra dell’1.
  6. [1, 2, 3, 4, 5] Visto che non ci sono più elementi da considerare, l’algoritmo è terminato, è l’array è adesso ordinato.

La parte in grassetto è quella ordinata ad ogni passo dell’ algoritmo. Ecco una gif con un esempio di esecuzione, preso da Wikipedia ma velocizzato un po’:

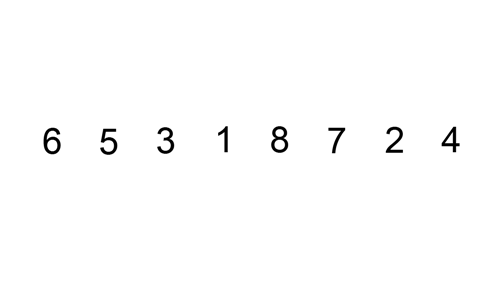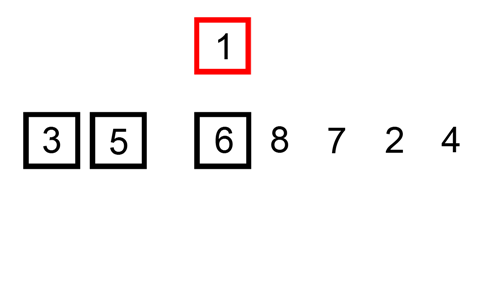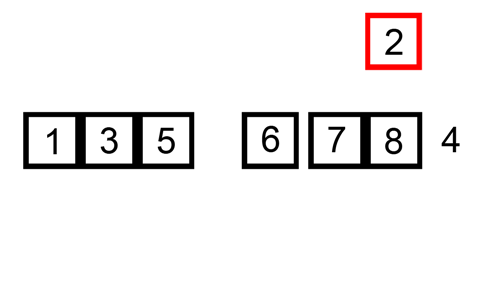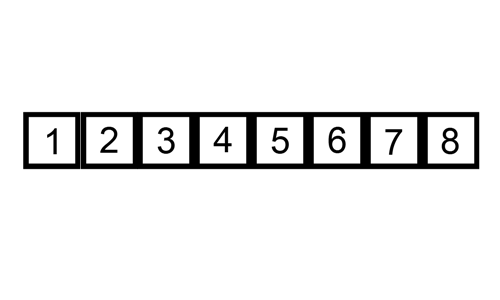
Pseudocodice dell’algoritmo Insertion Sort

Vediamo quindi uno pseudocodice dell’ algoritmo di ordinamento Insertion Sort:

for j=2 to length(A):
 chiave = A[j]
 i = j - 1
 while i > 0 and A[i] > chiave:
     A[i+1] = A[i]
     i = j-1
     A[i+1] = chiave

Un’altra caratteristica è la facilità di implementazione in praticamente qualsiasi linguaggio, richiedendo solamente l’array di input.

Codice dell’algoritmo Insertion Sort in Python3

Ecco una possibile implementazione dello pseudocodice, utilizzando python:

def insertionSort(arr):
    for i in range(1, len(arr)):
        val = arr[i]
        j = i - 1
        while j >= 0 and arr[j] > val:
            arr[j+1] = arr[j]
            j = j -1
        arr[j+1] = val
    return arr
 
import unittest
import random
 
class SortingTest(unittest.TestCase):
    def setUp(self):
        self.i = list(range(0, 100))
        self.sort = insertionSort
 
    def testOrdered(self):
        self.assertEqual(self.i, self.sort(self.i))
 
    def testReversed(self):
        self.assertEqual(self.i, self.sort(self.i[::-1]))
 
    def testUnordered(self):
        self.assertEquals(self.i, self.sort(random.sample(self.i, len(self.i))))
 
if __name__ == "__main__":
    unittest.main()